Assignment 6

Part 1

The goal of this assignment was to determine whether or not there is a relationship between the percent  of children receiving free school meals and crime rates per hundred thousand people. This is being conducted as a local radio station from the town in which the data was gathered suggested that as the number of children receiving free meals at school increases, so does the crime rate. SPSS was used to conduct regression analysis to determine whether or not there is truth to this.

For this test, the percentage of children receiving free school meals is the independent variable, while the depended variable is the crime rates per one hundred thousand people.

Figure 1 shows the results of the SPSS statistical test. From the Standardized Coefficients column, we can see that the result is .416. This result indicates that there is a linear relationship between the percentage of children receiving free school meals and crime rates. This result is significant, as we can see in the column labelled 'Sig.' that the significance is .005 - anything smaller than .05 would indicate significance, as the confidence level for this test is 95%. Therefore, there is a relationship between the two. However, this relationship is strong enough to be considered significant but is not particularly strong, as a result of  0 would indicate that no relationship is present - this result is not much higher than 0, but is still positive. Therefore, while there is a positive relationship between the two that is significant, meaning that as the percent of children receiving free school meals increases so does the crime rate per one hundred thousand people, this is not particularly strong.

Figure 1 - SPSS output showing the standardized regression coefficient between free school meals and crime rates, as well as the significance of the results.

The equation for calculating regression is Y = a - bX. In this case, a is 21.819, as seen in the 'Unstandardized B' column above, while b = 1.685. Therefore, the equation would be Y = 21.819 - 1.685X. With this in mind, we can calculate what the corresponding crime rate would be for a town with 23.5% of children receiving free school meals. The calculation for this would be Y = 21.819 - (1.685*23.5). The result of this is a crime rate of 39.5975 per hundred thousand people. However, when looking at the r-squared value associated with the test, we can see that this is .173 (figure 2). This is otherwise known as the coefficient of determination and measures how well the independent variable explains the dependent. This is measured on a scale of -1 to 0 to +1, with +1 and - 1 indicating 100% confidence and 0 indicating no confidence. Therefore, the number of free school meals is explaining 17% of the crime rate, which is not particularly high. The r-squared here is above 0, but is still very low which suggests that while the results are significant the independent variable of free school lunches does a poor job of explaining the dependent variable of crime rates, which means that the calculated result above may not reflect reality.

Figure 2 - Model Summary from SPSS output showing r-squared value and standard error of estimate.

Part 2

Introduction

The goal of this section of the task is to advise a company on where in the city of Portland, Oregon, is the best location to place an ER, based on the number of 911 calls recieved per census tract and the factors influencing the number of calls. This is also useful to the City of Portland, who are interested in identifying the reasons contributing to the number of calls. The factors that they are primarily interested in examining the influence of are: unemployment; low education; and college graduates. Additional variables that could also contribute to a higher number of 911 calls are also of interest the City, which will help them make sure they have adequate response teams available based on each area.

Methods

First, three single regression analyses were conducted using SPSS with the dependent variable being number of calls, and the independent variables being: unemployment; low education; and college graduates. As there are additional factors that could influence the number of calls made from within a census tract, a multiple regression was completed that looked at these additional factors, such as the number of renters and number of people born in a foreign country. These were then mapped using residual maps. Next, multiple factors were analysed using multiple regression to see which had the largest impact on the number of calls made. A multicollinearity diagnostic was used to check that the results were accurate.

Results

Low Education - Figure 3 shows that there is a positive relationship between the number of people with low education levels and the number of 911 calls, which is significant as the significance value is .000 which is lower than .05. This being the case, we can reject the null hypothesis as there is a linear relationship between these variables. This suggests that as the number of people with low education levels in an area increases, so does the number of 911 calls. The equation for this would be Y = 3.931 - 0.166X. Therefore, for every unit of change (increasing the low education rate by one), we would see an increase of .166 in the number of 911 calls placed. Figure 4 shows us that the r-squared value is .567, which indicates that low education rates are explaining 56% of the variation in numbers of 911 calls.

Figure 3 - Coefficients table showing the regression analysis results between the number people with low education levels and 911 calls.

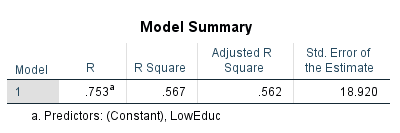Figure four - Model summary of the regression between people with low education levels and 911 calls. 

 Percent College Graduates - Figure 5 shows that there is a negative linear relationship between the percentage college graduates in a census tract and the number of 911 calls. However, the significance result of .142 indicates that this result is not significant, so in this case we would have to fail to reject the null hypothesis, meaning that there is no linear relationship between the percentage of college graduates and the number of 911 calls. We can see from figure 6 that there is a very small r-squared value, of only 0.25, which shows that the number of college graduates can only explain 2% of the 911 calls. This highlights the fact that the percentage of college graduates in an area does not significantly contribute to the number of 911 calls made.

Figure 5 - Coefficients table showing the relationship between percentage of college graduates and 911 calls.

Figure 6 - Model Summary of the regression between percentage of college graduates and number of 911 calls.

 Unemployment - Figure 7 shows that there is a positive linear relationship between the unemployment rate and number of 911 calls in census tracts in Portland. The significance of this is .000, which is lower than .05 and means that we can reject the null hypothesis and state that as the unemployment level increases, so does the number of 911 calls. The equation associated with this result is Y = 1.106 - .507X. Therefore, for every one unit of change in the unemployment rate, we would expect to see and increase in the number of 911 calls by .507.  From figure 6, we can see that with an r-squared value of .543, the unemployment rate is explaining 54% of the variation in number of calls.

Figure 7 - Coefficients table showing the results of the regression analysis between unemployment rates and number of 911 calls. 

Figure  8 - Model Summary of the regression between unemployment rates and number of 911 calls. 

From this, we can see that unemployment rates and low education rates have a linear relationship with the number of 911 calls placed, but the percentage of college graduates in an area does not. From the map below (Figure 9), we can see that the areas with the highest number of 911 calls are mainly in the north of the city, with the lowest number of calls on the outskirts of the city. which suggests that, from these results, we may expect to find higher levels of unemployment and low education compared with the other census tracts in the city of Portland, for instance the area in the north of the state including tracts 59 - 66.

Figure 9 - Map showing the number of calls from each census tract in Portland, Oregon

As the Low Education variable has the highest r-squared value (.567), a residual map was created based on this.

Figure 10 - Residual Map

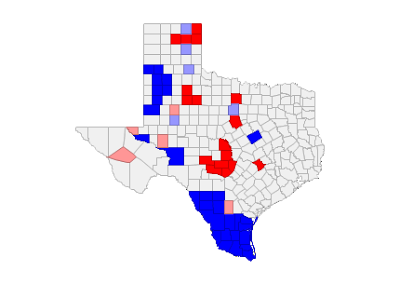
From the map above, we can see how far from a line of best fit each tract plot point would fall on a graph. Those closest to the line of best fit are beige, while those in blue have a residual that means they are lower than the line of best fit, while those in blue are higher, and in the red are below the trend line. This shows how these areas deviate from the model created.


In addition to the three factors explored above, multiple regression analysis was used to identify other factors contributing to the number of 911 calls. These were: Jobs, Renters, LowEduc (Number of people with no HS Degree), AlcoholX (alcohol sales), Unemployed, ForgnBorn (Foreign Born Pop), Med Income, CollGrads (Number of College Grads). Figure 11 shows the Coefficient table with the results of the multiple analysis. With an r-squared value of .780, we can see that the variables are doing a good job of explaining the number of calls made (Figure 11).

Figure 11 - Multiple Regression coefficients table

Figure 12 - Multiple regression model summary.

From figure 11, we can see that a number of the factors have a significance of above .05, meaning that they are not significant and there is no linear relationship between these factors and the number of 911 calls. These are: renters; unemployed; foreign born; median income' and college graduates. This suggests that the only significant factors contributing to the number of calls made are low education and jobs. However, figure 12 shows a relativley high r-squared of .760, indicating that the independent variables are doing a good job of explaining the dependent variable.  This seems unusual, so a diagnostic test was used to check for multicollinearity.
When conducting multiple regression analysis, it is important to check for multicollinearity as this occurs when two of the independent variables correlate highly with one another, which can make the results of the multiple regression redundant. This could make an independent variable that would be significant on its own appear to be insignificant.  Figure 13 shows the results of this diagnostic test. As the condition index values are below 30, this indicates that no multicollinearity is present. This means we can continue with the results shown above.

Figure 13 - Multicollinearity diagnostic.

 To identify which of these variables were the most important, a stepwise approach was also used: this method of doing a multiple regression sorts through the data and picks out the three independent variables that have the largest influence on the dependent variable. These are; Renters, Low Education and Jobs (Figure 13). It is interesting, as here, renters is significant. This suggests that despite the condition index values being below thirty, some level of multicollinearity was occurring in the previous test that made it appear that the number of renters was not significant. Figure 14 shows that jobs has the highest r-squared value, so this is the variable that has the most influence on the number of 911 calls placed (Figure 14).

Figure 14 - Stepwise regression coefficients table

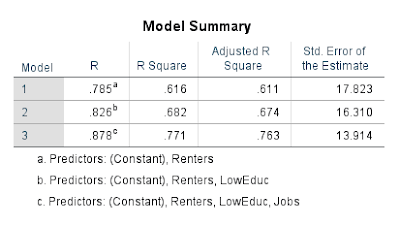Figure 15 - Stepwise regression model summary.

Conclusion



The number of calls made to 911 in the city of Portland, Oregon, is influenced by many factors, particularly the jobs in the tract, the number of renters and the number of low education individuals. These results are interesting and will help the city of Portland to plan where a new ER would be best located - ideally in easy reach of areas with a high percentage of renters, low education individuals and those with jobs. This will mean that those who need to access the service most will have shorter travel times. From the map in figure 9, the tracts in the northern area of the city would appear to be a suitable location as these are areas where the highest number of calls has already been identified to be coming from.

Assignment 5

Part 1

The goal of this part of the assignment is to be able to use SPSS statistical software to run correlations and make correlation matrices, and interpreter the results.

Figure 1 shows a correlation matrix made using SPSS, which shows the correlation between different racial groups, median household income and job sectors.

For context, the data categories were as follows, all from Milwaukee County:
White - White population for the Census Tracts
Black - Black population for the Census Tracts
Hispanic - Hispanic population for the Census Tracts
MedInc - Median Household Income
Manu - Number of Manufacturing Employees
Retail - Number of Retail Employees
Finance - Number of Finance Employees

Figure 1 - Correlation Matrix made using SPSS, showing correlation between race and job sector in Milwaukee, Wisconsin.

Using the above chart, and a significance level of 95%, we can reject the null hypothesis (that there is no correlation between two variables) where the matrix shows the significance to be anything below .05. If the significance is greater than this value, we must fail to reject the null hypothesis. We can also use SPSS's star rating system to find out if there is a correlation between variables - one star (*) indicates that the correlation is significant to 0.05 level, while two start (**) indicates there is a stronger correlation between the variables - one which is significant to the 0.01 level, or 99% confidence.

From the results, we can see that there is a correlation between the number of manufacturing jobs and retail employees, and finance employees. Likewise, there is a correlation between the number of financial employees and retail employees.

In the financial sector, there is a positive correlation between white people and number of finance employees, and a negative correlation between black and hispanic people and finance employees. This could be because of societal prejudice against black and hispanic people in Milwaukee county, and could also be due to the fact that less people from these racial groups have access to the higher education opportunities that would allow them to become employed in the financial sector.

Interestingly, there is a negative correlation between the number of black people in a census tract and the number of white or hispanic people in the census tract. Milwaukee is well known to be the most racially segregated city in the United States, and these statistics seem to hold true to this. This suggests that areas of Milwaukee where the black population live tend to be majority black areas. There is, however, a positive correlation between the number of white people and hispanic people in Milwaukee census tracts, which suggests that the African American population in Milwaukee is more segregated than the White or Hispanic populations.

Part 2

For the second part of assignment 5, we were asked to prepare a report for the Texas Election Commission.

Introduction

The Texas Election Commission (TEC) has tasked us with analyzing election data from the years 1980 and 2016, based on election turn out and percentage democratic vote, in order to establish whether or not patterns exist. Furthermore, they have requested that we look into settlement patterns of Hispanic people from the 2015 census, to see if there is any pattern between this and the voter turnout and percent Democrat vote. This will allow us to see how the distribution of Hispanic populations affects elections in Texas, as well as how voting patterns have changed in the state over the thrity-six year period between 1980 and 2016.

Methods

Results were achieved using data provided by the TEC showing voter turn out and percent Democratic vote and data downloaded from the US census bureau's 2015 concerning the Hispanic population in Texas counties.

SPSS software was used to create a correlation matrix with the data provided by the TEC, to give a preliminary indication of whether or not there has been a change in election patterns between the 1980 election and the 2016 election. SPSS was also used to look for a correlation between the percentage Hispanic population and the 2016 election data they provided.

To give spatial context to these results, GeoDa was used to create Local Indicators of Spatial Autocorrelation maps, otherwise known as LISA maps. These maps are based on the principal of Moran's I, which compares the values of a variable at one location, in this case within a county, to the value of the same variable at another location. When displayed on a LISA map, this can give a clear indication where clustering occurs. The LISA mpas were created using a shapefile for Texas counties downloaded from the US Census Bureau.

Results

Figure 2 shows the correlation matrix for the voter turn outs and percentage Democrat vote from the 1980 and 2016 elections.

Figure 2 - correlation matrix showing the strength of correlation between the voter tun out and percentage democratic votes from 1980 and 2016.

Using a two tailed test at 95% significance, we can see there is a positive correlation between voter turn outs of 1980 and 2016 (.525) . This suggests that in areas where there was a high voter turnout in 1980, this pattern has continued into 2016 and vise versa.

There is, however, a negative correlation between voter turn out and percent Democrat vote for both the 1980 and 2016 elections (-.612 and -.564 respectively). This indicates that as voter turnout increases, the percentage of votes won by the Democrats decreases. This suggests that between 1980 and 2016, the voters of Texas have been more likely to vote Republican.

To see how Hispanic voters affected this in the 2016 election, a correlation matrix was created using the 2016 data provided by the TEC and the data taken from the 2015 census to illustrate this (Figure 3).

Figure 3 - Correlation Matrix for Percent Democrat Vote 2016, Voter Turnout 2016 and Hispanic Population recorded during 2015 census across counties in Texas.

We can see that there is a strong positive correlation between the Hispanic population in Texas (column HD02_S02 on in figure 3) and the percent democratic vote for 2016. This suggests that the higher the percentage of Hispanic people in a county, the higher the democratic vote. There is a negative correlation between voter turnout and Hispanic population, which suggests that as the Hispanic population in a county goes up, the voter turnout goes down. This could suggest that Hispanic people are unlikely to vote in presidential elections.

In order to give spatial context to these results, GeoDa was used to look for clustering.Figure 4 shows the percentage democratic vote in 2016, while figure 5 shows the percentage democratic vote for 1980.

Figure 4 - LISA Map showing spatial auto-correlation of percentage democratic vote from the 2016 Texas presidential election.

Figure 5 - LISA Map showing spatial auto-correlation of percentage democratic vote from the 1980 Texas presidential election.

In the maps above, blue indicates that these are counties with high democratic votes surrounded by other areas of high democratic votes. The red indicates counties with low democratic votes surrounded by other counties of low democratic votes. The pale blue and red indicate that these counties are not similar to their surrounding counties. The grey counties do not have a significant spatial auto-correlation. This is illustrated in the legend GeoDa produces to go alongside the spatial auto-correlation maps (Figure 6).

Figure 6 - LISA Map Legend

It can be seen that since 1980, the democratic vote has remained high in the most northernly counties in Texas, and low in the most southern. However, there is no longer a significantly low number of democratic votes in the eastern area of the state that was significant during the 1980's, and the area of strong democratic support in the 1980's on the western border has become less significant and democratic strength has shifted east. This indicates that while some voter patterns in terms of the number of democratic votes have remained similar to 1980, this has not been true across the state as a whole.

Next, the following figures 7 and 8 show the spatial auto-correlations of the voter turnout across Texas for the years 2016 and 1980 respectively.

Figure 7 - LISA Map showing spatial auto-correlation of voter turn out across Texas counties for the 2016 Presidential election.

Figure 8 - LISA Map showing spatial auto-correlation of voter turn out across Texas counties for the 1980 Presidential election.

From figures 7 and 8, we can see that the south of the state has a consistently high voter turnout, as indicated by the dark blue color of the counties here. This has remained consistent between 1980 and 2016, and is also an area where the percentage Democratic vote has remained consistently low between 1980 and 2016, which suggests that this area of the state is a Republican stronghold.

The rest of the state does not show any areas that indicate a strong pattern between 1980 and 2016, aside from the are north of the aforementioned Republican stronghold, where votes are low and have remained consistently low.

Next, the voter turnout and percentage democratic vote was compared with the Hispanic population of the state (Figure 9).

Figure 9 - LISA Maps showing, from left to right:  Percentage democratic vote, 2016; Voter Turnout, 2016; and Hispanic Population, 2015. 

From the comparison above, we can see the most prominent area of high Hispanic population is the cluster of dark blue counties in the east of the state. where the dark blue indicates that these counties have a high Hispanic population and are surrounded by other counties with high Hispanic population. However, this area on the percentage democrat vote map and voter turnout map is predominantly grey, indicating that there is no significance. This suggests that the Hispanic population did not have much of an influence on the election results in Texas in 2016, whereas the areas of the state with low Hispanic population along the south west border have low numbers of democrat voters and high voter turnout, will have had more influence on the outcome of the election.

Conclusion

While spatial patterns are evident between the voter turnout and percentage democrat votes in Texas, as can be see from both the SPSS correlation matrix and the LISA maps, the Hispanic population do not appear to have a significant impact on the result of elections, as shown by the grey colour on the LISA maps that indicate areas of high Hispanic population are not significant in terms of democrat votes. This is despite the fact that the SPSS correlation shows there is a positive correlation between the number of Hispanic people in a county and the percentage Democrat vote. This suggests that despite Hispanic people being more likely to vote Democrat, they do not have much of an influence on the overall outcomes of elections.

Sources
http://www.governing.com/topics/politics/gov-milwaukee-most-segregated-polarized-place.html
US Census Bureau.
Texas Election Commission.

Assignment 4

Part 1: Z and T Tests

1. The following table shows the z and t values associated with various hypothetical tests, which are either one or two tailed and have varying confidence levels.

	Interval Type	Confidence Level	n	a	z or t?	z or t value
A	Two Tailed	90	45	0.05	Z	1.65
B	Two Tailed	95	12	0.025	T	2.201
C	One Tailed	95	36	0.05	Z	1.65
D	Two Tailed	99	180	0.005	Z	2.58
E	One Tailed	80	60	0.2	Z	2.06
F	One Tailed	99	23	0.01	T	2.508
G	Two Tailed	99	15	0.005	T	2.977

2.  An organization from the Kenyan Department of Agriculture and Live Stock Development has created estimates for the yields of Ground Nuts, Cassava and Beans in a certain district, based on the average yields of the country as a whole. Per hectare, it is expected that 0.57 metric tons of groundnuts, 3.7 metric tons of cassava and 0.29 metric tons of beans can be produced. 

To test whether these estimates are realistic, a survey of 23 farmers was carried out. The results were as follows 

      μ              σ

                  Ground Nuts  0.52         0.3

                  Cassava          3.3           0.75

                  Beans             0.34         0.12

To see whether or not these results were statistically different from the average yields from the three crops mentioned above, hypothesis testing was carried out. 

Ground Nuts

Null Hypothesis: There is no difference between the average yields of ground nuts in the selected area and the average yields for the country as a whole

Alternative Hypothesis: There is a difference between the average yields of ground nuts in the selected area and the average yields for the country as a whole. 

Statistical Test: A T test, or Student's T test was chosen to perform the statistical analysis, due to the fact that this type of test is better suited to samples with a small number of observations, and here our number of observations is below thirty as only 23 farmers were sampled. 

Confidence Level: For all three tests, a confidence level of 95% was chosen. As we are conducting a two tailed test, the alpha level is 0.025. This means the critical value, based on 23 degrees of freedom, will be ±2.069 Thus, for this test and the two that follow, a T test result of less than 2.069 but greater than -2.069 will cause us to fail to reject the null hypothesis, meaning that there is no statistical difference between the average yields for this particular area compared to Kenya as a whole. If the result does fall to either side of the critical values rather than between them, we must reject the null hypothesis. This means that there is a statistical difference between the average yields in this area compared to Kenya as a whole. 

T test result: -0.365.

Conclusion: This result is lower than the critical value of 2.069, but greater than -2.069, meaning it does not fall within either of the two tails. Therefore, we must fail to reject the null hypothesis. The probability of this result occurring is 35.94%

Cassava

Null Hypothesis: There is no difference between the average yields of cassava in the selected area and the average yields for the country as a whole

Alternative Hypothesis: There is a difference between the average yields of cassava in the selected area and the average yields for the country as a whole. 

Statistical Test: T test.

Confidence level: 95%

T test result: -2.564

Conclusion: The result of -2.564 is less than the critical value of -2.069 on the left tail. Therefore, we must reject the null hypothesis. The probability of this result occurring is 0.54%

Beans

Null Hypothesis: There is no difference between the average yields of beans in the selected area and the average yields for the country as a whole

Alternative Hypothesis: There is a difference between the average yields of beans in the selected area and the average yields for the country as a whole. 

Statistical Test: T test.

Confidence Level: 95%

T test result: 1.998

Conclusion: This result is lower than the critical value of 2.069 but greater than -2.069, meaning it does not fall within either of the two tails. Therefore we must fail to reject the null hypothesis. The probability of this result occurring is 2.33%

In light of these results, it is clear than while there is no statistical difference between he average yields of beans and ground nuts in the particular area when compared to the country as a whole, is a statistical difference between the amount of Cassava produced. The T test result falls within the left tail, and is negative, meaning that there is statistically less cassava produced in each yield in this part of the country compared to Kenya as a whole. This means that it may be difficult for farmers in this area to get close to the estimated cassava yield provided by the Department for Agriculture and Live Stock Development. This could be due to changes in soil quality or climactic conditions in theis area that do not favor the growth of cassava, resulting in smaller yields for farmers here.

3. As a researcher suspects the level of pollutants in a particular stream to be higher than the allowable level of 4.2mg/l, 17 samples were taken, and from these a mean pollutant level of 6.4mg/l were found, with a standard deviation of 4.4. Hypothesis testing was carried out to find out if this sample was statistically different from the rest of the stream.

Null Hypothesis: There is no difference between the levels of pollution in the sample and the rest of the stream.

Alternative Hypothesis: There is a difference between the levels of pollution in the sample and the rest of the stream. 

Statistical Test: A T test shall be used, as we have a relatively small sample size of 17 and this test is better suited to small samples than a Z test.

Confidence level: 95%. This is a one tailed test, so the alpha level is therefore 0.05. Based on 16 degrees of freedom, this means that the critical value is 1.746. If the calculated test result is greater than this value, we will reject the null hypothesis. If it does not exceed this value, the we will fail to reject the null hypothesis.

Test results: 2.062

Conclusion: As the test result of 2.062 is greater than the critical value of 1.746, we must reject the null hypothesis. This means that statistically, the samples taken from the stream are more polluted than the allowable level of 4.2mg/l. 

The probability of this value is 1.97%

Part 2

For this part of the assignment, we are looking to find out whether or not there is a statistical difference between the home values in Eau Claire City block groups, compared to all of the block groups in Eau Claire County.

To do this, hypothesis testing was carried out, as follows:

Null Hypothesis: There is no difference between the average house values of homes in Eau Claire City block groups compared to the block groups of Eau Claire Country as a whole.

Alternative Hypothesis: There is a difference between the average house values of homes in Eau Claire City block groups compared to the block groups of Eau Claire Country as a whole.

Statistical Test: A Z test was chosen as the appropriate statistic, This is due to the fact that we have a sample size of 53, as there are 53 block groups in Eau Claire city. This shall be a one tailed test. 

Confidence Level: 95%. As this is a one tailed test, the alpha level is thus 0.05. From this, we can figure out a critical value of 1.65. If out test statistic exceeds this, we must reject the null hypothesis.

Test result: 2.572.

Conclusion: As the test result of 2.572 is greater than the critical value on 1.65 associated with our one tailed test, we must reject the null hypothesis. This means that the value of houses located within the block groups that make up the City of Eau Claire is statistically different from the value of houses in the rest of the county.

Figure 1 - Map showing the block groups of Eau Claire by average house value, with City of Eau Claire block groups in bold.

From figure 1, it is clear that many of the block groups within the City of Eau Claire have a lower average property value, particularly as the block groups get smaller in the central business district area. This could be because properties here tend to be smaller, and those in urban areas are likely to have less green space and could lack other amenities such as parking availability if they are apartments. Furthermore, the area is also the location of both the University of Eau Claire and Chippewa Valley Technical College. This means that many of the properties are student rentals, and are not as well maintained as other homes. This would drive down the value of the property compared to those properties not intended to be student rentals. Lastly, this area is also in the vicinity of the Chippewa River, which runs through the city's downtown area. Properties that fall within the potential flood plain of the Chippewa River will also be likely to have lower values due to the potential for future floods and preexisting flood damage.